358ナンバーの続き2
フィボナッチを知るきっかけとなったのが、通常、5、25、50、200日線と言われる株式でいうところのグランビルの法則を勉強した時だった。
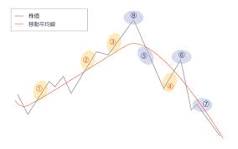
トレードを学んでいるときにフィボナッチ数列を知り、5、25、50、200を3、5、8、21と短い期間でやり取りすることを覚えた。知れば知るほど不思議というか自然界はフィボナッチで成り立っているし、身近なところにもフィボナッチの数列が存在する。
フィボナッチから作られる「螺旋形状」
木の葉やDNA螺旋…にもみられることが分かる。
「松ぼっくり」や「ひまわりの種」の並び方は「螺旋(らせん)形」です。この形状は強度を保つため、効率的に成長するのに合理的であり、植物が自然界で生存するために必然的に現れたものであり、「生命の曲線」と言われています。

これもフィボナッチ数列に関連しています。下図のように1辺の長さが「1、1、2、3、5、8、13、21、…(フィボナッチ数列)」の四角形を並べると渦巻き状に並べることが出来ます。正方形の辺を半径とした円を描くと「螺旋(らせん)」が広がっていきます。
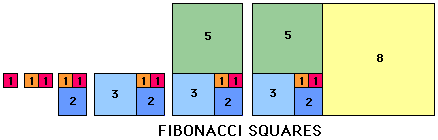
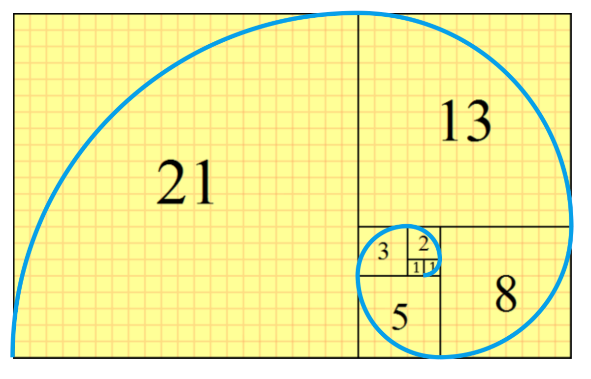
この「螺旋(らせん)」の形状は自然界であらゆるところで観察されます。
「植物の葉」は茎の成長と共に「螺旋状」に葉を付け、茎を中心にして2方向、3方向、5方向、8方向に生えていきます。この生え方をすることによって、自然と葉同士が重ならずに、光合成の効率を上げるようになっています。https://forest-clinic.jp/ 抜粋
まだまだ続きます。